1、二叉树

2、二叉搜索树

3、平衡二叉树之AVL树

4、平衡二叉树之红黑树

5、BTree

6、B+Tree

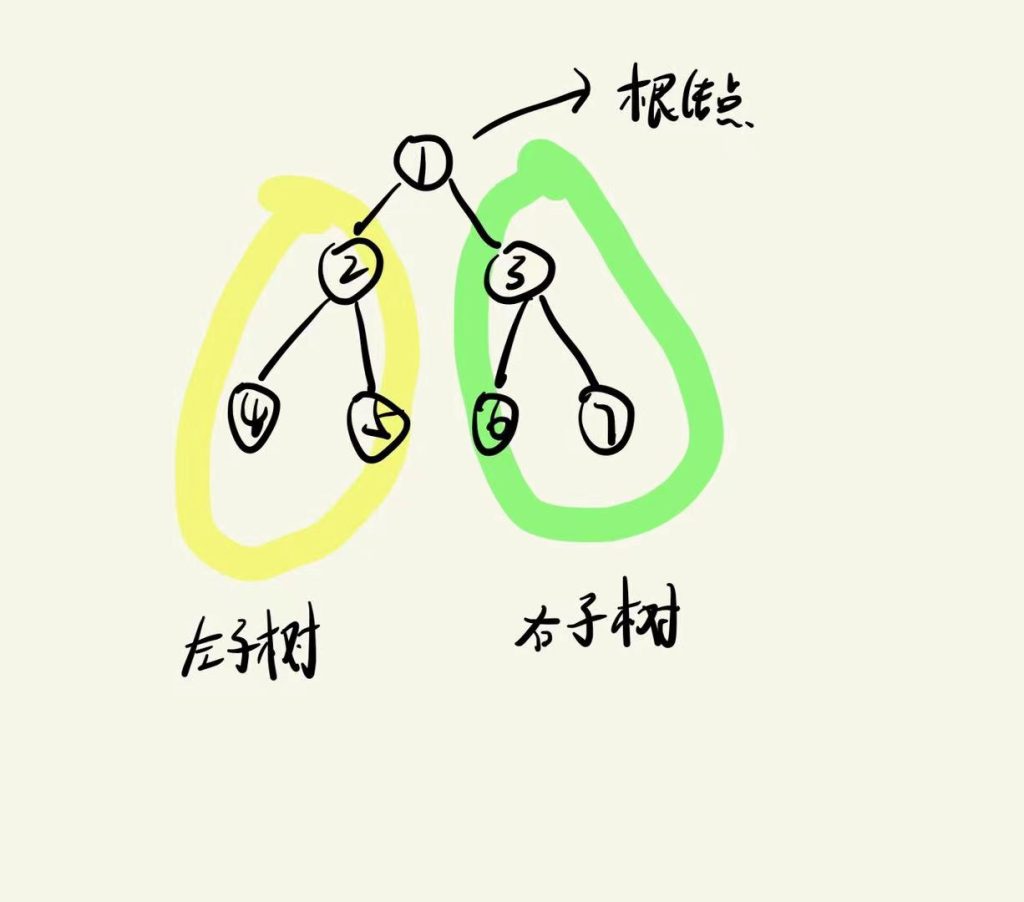
一、二叉树

一种树形结构，每个节点最多有2个子节点，分别为左子结点和右子节点，是其它高级数据结构的基础（如平衡二叉树、二叉搜索树等）。

特殊的二叉树有满二叉树和完全二叉树。

满二叉树：非叶子节点都有两个子节点，且叶子节点都在同一层。（全满）

完全二叉树：除最后一层外，其余层的节点数都达到最大值。且最后一层节点从左到右连续排列。（不满但不缺漏）

二叉树的遍历方式（即按某种规则访问树中所有节点且仅访问一次）：

①前序遍历：先访问根节点，再遍历左子树，最后遍历右子树。

②中序遍历：左——>根——>右

③后序遍历：左——>右——>根

二、二叉搜索树

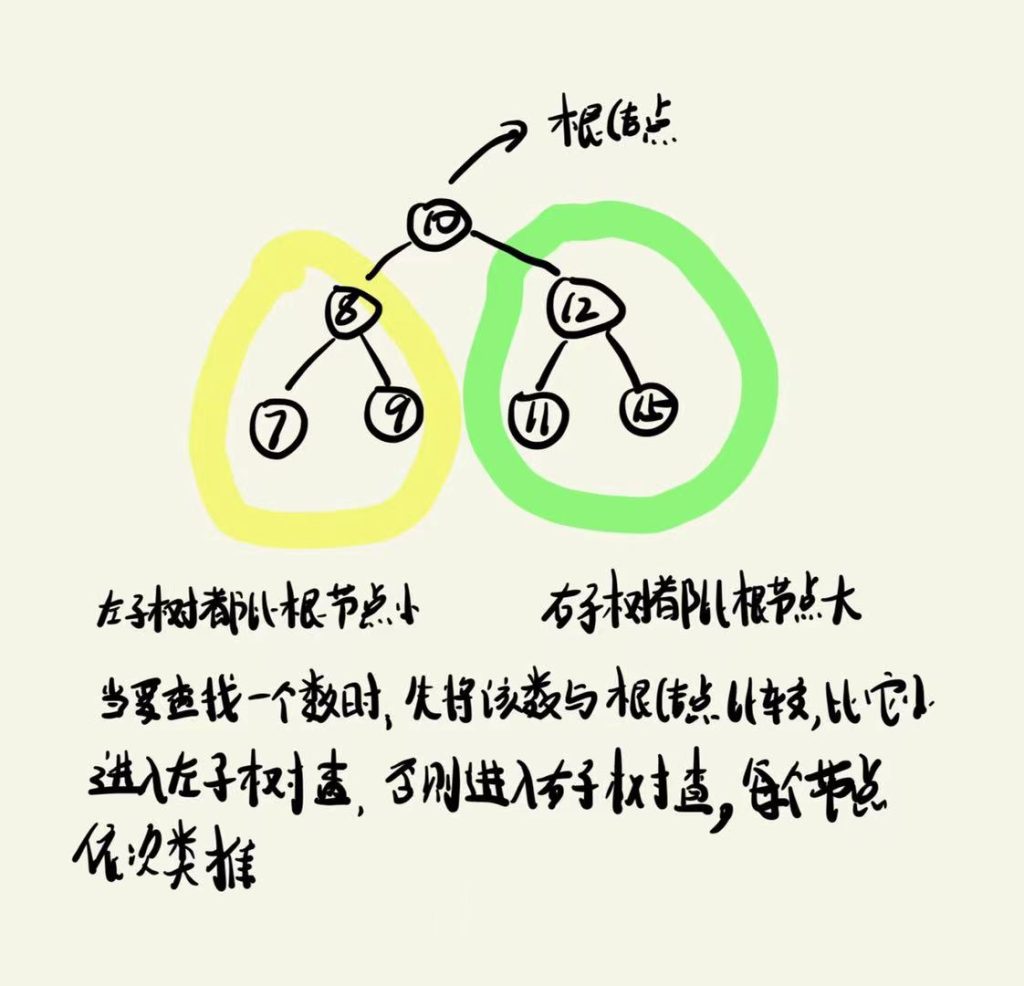
又称二叉排序树、二叉查找树，是在二叉树的基础之上衍化而来，在继承二叉树的性质同时，还有自己独特的性质。相关性质有：

①左子树节点值小于该节点。

②右子树节点值大于该节点。

③左右子树都为二叉搜索树。（常假设树中节点值唯一）

理想情况：树的高度平衡（如完全二叉树），查、插、删均为O(logn)

最坏情况：当节点按升序或降序插入时，会退化为链表，此时为O(n)

三、平衡二叉树之AVL树

平衡二叉树是一种特殊的二叉搜索树，特点是通过维持树的 “平衡性”，避免普通二叉搜索树在极端情况下退化为线性结构（O(n)），从而保证查找、插入、删除等操作的高效性（O(log n)）。

AVL树是最早的平衡二叉树，是 “严格平衡” 的二叉搜索树（平衡因子严格限制为 – 1、0、1）。每个节点的左右子树高度差不能超过1。

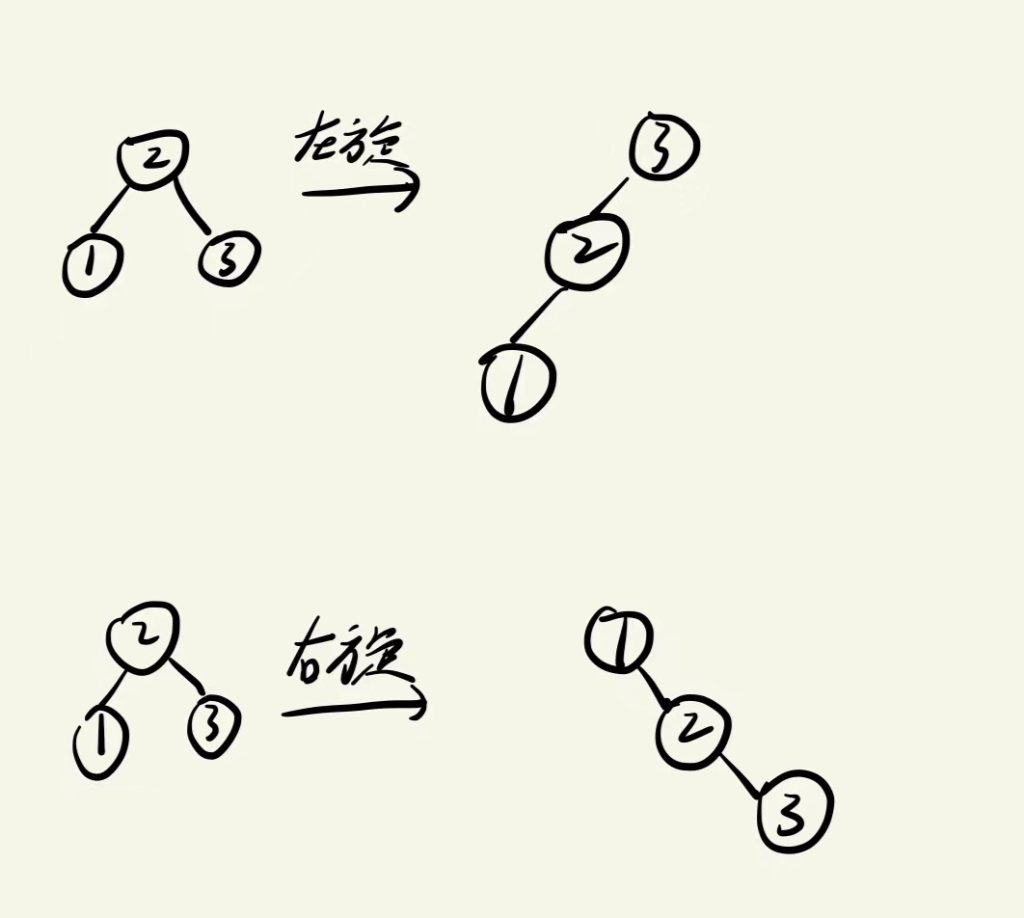
AVL 树的插入、删除可能破坏平衡性，需通过旋转操作调整结构以恢复平衡，而旋转的目标是降低树的高度。

左旋：以某个节点为旋转节点，其右子节点变为父节点，原来的父节点变为左子结点。

右旋：同理，左子结点变为父节点，原父节点变为右子节点。

缺点：相比较红黑树，AVL树在插入/删除时会频繁触发旋转操作，从而来达到树的高度平衡，这会导致耗时比红黑树高。

四、平衡二叉树之红黑树

一种 “弱平衡” 二叉搜索树（通过颜色规则维持平衡，平衡因子可大于 1(即左右子树的高度差可大于1)），插入 / 删除的旋转操作更少，适合频繁修改的场景（如 Java 的TreeMap、HashMap（JDK8+）。相关性质：

①每个节点要么是红色，要么是黑色。

②根节点是黑色的。

③叶子结点都是黑色的NULL节点。

④若一个节点为红色，其两个子节点一定为黑色。

⑤任意节点到其可到达的叶子结点之间有相同数量的黑色节点。

实现自平衡的方式——>变色+旋转。

推论：从根到叶子结点的最长路径不大于最短路径的2倍。

即树高控制在 2log (n+1) 以内，确保操作效率稳定在 O (log n)。

五、BTree

一种多路平衡搜索树，每个节点可以存储多个数据元素，并拥有多个子节点（二叉树的每个节点最多存储1个元素且最多有2个子节点）。优势是降低树的高度，减少访问数据时的磁盘读写次数。

B 树的阶（通常用m表示）是其核心参数，指的是一个节点最多能拥有的子节点数。一棵m阶 B 树需满足以下条件：

①每个节点最多包含m-1个关键字（数据元素），以及m个子节点。

②若一个节点存储的元素超过最大值，则中间元素向上分裂成父节点，左右两边元素分裂成左右子节点。

③非根非叶子节点至少存在向上取整（m/2）个子节点。

④树中所有叶子节点到根节点的路径长度相等。

优势：

1、低高度：多路节点结构使树的高度远低于二叉树，减少磁盘 I/O 次数。（树的高度决定检索的次数）

2、所有叶子节点在同一层，保证查询、插入、删除操作的时间复杂度均为O(log n)

六、B+树

是 B 树的变种，两者核心区别在于：

①B+树的非叶子节点仅作为索引，不存储实际数据，所有关键字和数据都存储在叶子节点中。

②B+树的叶子节点通过链表连接，支持范围查询，而B树可能需要遍历多个层次的节点才能完成范围查询。

为什么数据库索引用B+树，而不用B树？

1、进行范围查询时，B+树只需从根节点定位到叶子结点的范围起点，然后顺序扫描链表就能遍历后续数据，非常高效。而B树可能要在不同层次的节点间多次跳转查找，无疑增加了查询的时间和复杂度。

2、更适合顺序访问，B+树可通过链表快速定位和访问相邻数据，而B树没这优势。

3、减少非叶子结点的存储开销，B+树的非叶子节点仅包含键信息，不包含数据，使得非叶子节点可以存储更多的键，从而减少树的高度。B树的非叶子节点既包含键又包含数据，相比之下，每个节点能存储的键的数量相对较少，导致树的高度可能更高。